巧用加法原理和乘法原理解题

概要：;…4个，因此共有5种可能。质因数3在n的质因数分解式中可能不出现，也可能出现1个、2个，因此有3种可能。质因数5在n的质因数分解式中可能不出现，也可能出现1个，因此有2种可能。所以约数的个数：5×3×2=30（个）所有约数的和就是30个约数的和，即等于=31×13×6=2418例2 在下面的图中（单位：厘米）求：（1）一共有几个长方形？（2）所有这些长方形面积的和是多少？解（1）AE这条线段上有多少条线段就是长有多少种取法，很明显得出长有10种取法；同理，宽也有10种取法。一共有（10×10=）100（个）长方形。解（2）长的长度有10种：5、12、8、1、17、20、9、25、21、26，宽的长度也有10种：2、4、7、3、6、11、10、13、14、16。所有这些长方形的面积和=（5+12+8+1+17+20+9+25+21+26）×（2+4+7+3+6+11+10+13+14+16）=144×86=12384（平方厘米）练习：图中有6个点，9条线段，一只甲虫从A点出发，要沿着某几条线段爬到F点。行进中，同一个点或同一条线段只能经过一次，这只甲虫最多有多少种不同的走法？

巧用加法原理和乘法原理解题,http://www.daertutu.com

　　加法原理和乘法原理是两个最基本的计数原理。熟练地掌握这两个原理，有助于我们解决一些与计数有关的问题。

　　例1 720有多少个约数？所有约数的和是多少？

　　解 720=24×32×5，因此，720的任一约数都只能含有质因数2，3和5，对于720的某个约数n，只要研究它所含质因数2、3、5的个数。质因数2在n的质因数分解式中可能不出现，也可能出现1个、2个……4个，因此共有5种可能。质因数3在n的质因数分解式中可能不出现，也可能出现1个、2个，因此有3种可能。质因数5在n的质因数分解式中可能不出现，也可能出现1个，因此有2种可能。

　　所以约数的个数：5×3×2=30（个）

　　所有约数的和就是30个约数的和，即等于=31×13×6=2418

　　例2 在下面的图中（单位：厘米）

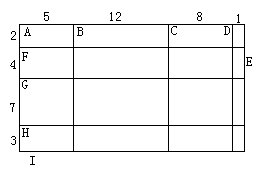
　　求：（1）一共有几个长方形？
　　（2）所有这些长方形面积的和是多少？

　　解（1）AE这条线段上有多少条线段就是长有多少种取法，很明显得出长有10种取法；同理，宽也有10种取法。

　　一共有（10×10=）100（个）长方形。

　　解（2）长的长度有10种：5、12、8、1、17、20、9、25、21、26，宽的长度也有10种：2、4、7、3、6、11、10、13、14、16。所有这些长方形的面积和=（5+12+8+1+17+20+9+25+21+26）×（2+4+7+3+6+11+10+13+14+16）=144×86=12384（平方厘米）

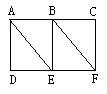
　　练习：图中有6个点，9条线段，一只甲虫从A点出发，要沿着某几条线段爬到F点。行进中，同一个点或同一条线段只能经过一次，这只甲虫最多有多少种不同的走法？